Zuren en Basen
1. Inleiding
Iedereen die zure snoepjes heeft gegeten of frisdrank heeft gedronken heeft wel eens ervaren hoe onze smaakpapillen reageren op iets dat zuur is. De zeep die we gebruiken om onze handen te wassen zijn basen, maar wat houdt dat eigenlijk allemaal in? Om dit te begrijpen zal in de eerste secties het evenwicht van water worden behandeld. Vervolgens zal worden gekeken wat er gebeurt wanneer een zuur of een base wordt toegevoegd aan een waterige oplossing waarin het begrip pH (zuurtegraad) zal worden toegelicht.
1.1. Evenwicht van water
De bijzondere eigenschappen van water is dat het zouten ioniseert in oplossing. Maar niet alleen zouten worden geïoniseerd, watermoleculen ioniseren elkaar ook volgens onderstaande vergelijking.
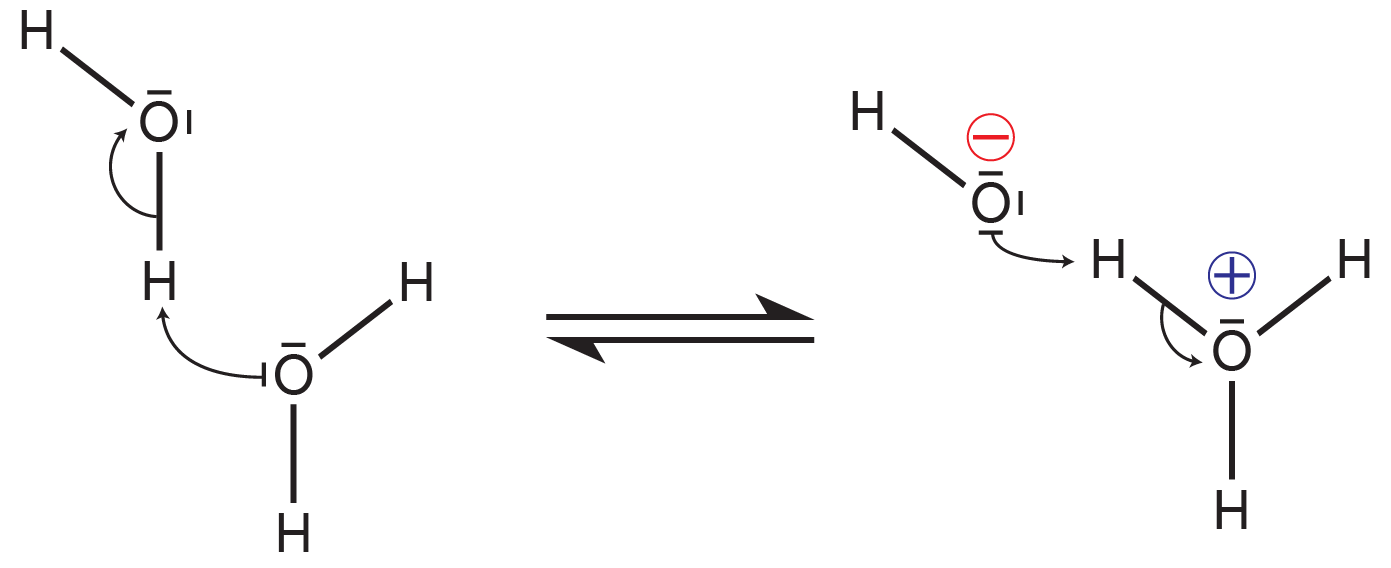
Dit proces is in evenwicht. Zoals aan de linkerkant van de vergelijking is te zien zijn er evenveel hydroxonium ionen \( \mathrm{(H_{3}O^{+})} \) als hydroxyl ionen \( \mathrm{(OH^{-})} \). In termen van concentraties (weergeven in vierkante haakjes) kan deze vergelijking als volgt worden geformuleerd: \[ \mathrm{2 [H_{2}O]⇌[H_{3}O^{+}]+[OH^{-} ]} \] Dit evenwicht kan worden omschreven met de evenwichtsvoorwaarde: \[ \mathrm{K_w =\frac{[OH^− ][H_3 O^+ ]}{[H_2 O]^2}} \] Gezien water ons oplosmiddel is kunnen we [H2O] gelijk stellen aan 1. Dit betekent dat de evenwichtsvoorwaarde kan worden herschreven als: \[ \mathrm{K_w=\frac{[OH^− ][H_3 O^+ ]}{1^2} =[OH^− ][H_3 O^+ ]} \] Oftewel, de evenwichtsvoorwaarde is gelijk aan de product van het aantal \( \mathrm{(H_{3}O^{+})} \) ionen en \( \mathrm{(OH^{-})} \) ionen. Gezien de concentraties gelijk zijn \[ \mathrm{[H_3 O^+ ]=[OH^− ]=1⋅10^{−7} mol \cdot L^{−1}} \] \[ \mathrm{K_w =(1⋅10^{−7} )^2=1⋅10^{−14}} \] In andere woorden, de concentraties van beide ionen in een zuivere oplossing zijn \( \mathrm{10^{-7} mol \cdot L^{-1}}\). Als we er even vanuit gaan dat de temperatuur constant blijft en er geen stoffen worden toegevoegd, dan blijft de evenwichtsvoorwaarde \( \mathrm{K_w} \) constant, dus deze verandert niet. Daarom kunnen we deze formule gebruiken om de concentratie \( \mathrm{(H_{3}O^{+})} \) of \( \mathrm{(OH^{-})} \) te berekenen. \[ \mathrm{1⋅10^{−14}=[OH^− ][H_3 O^+ ]}\] \[ \mathrm{[H_3 O^+ ]=\frac{(1⋅10^{−14})}{[OH^− ]} ,[OH^− ]=\frac{(1⋅10^{−14})}{[H_3 O^+ ]}} \]
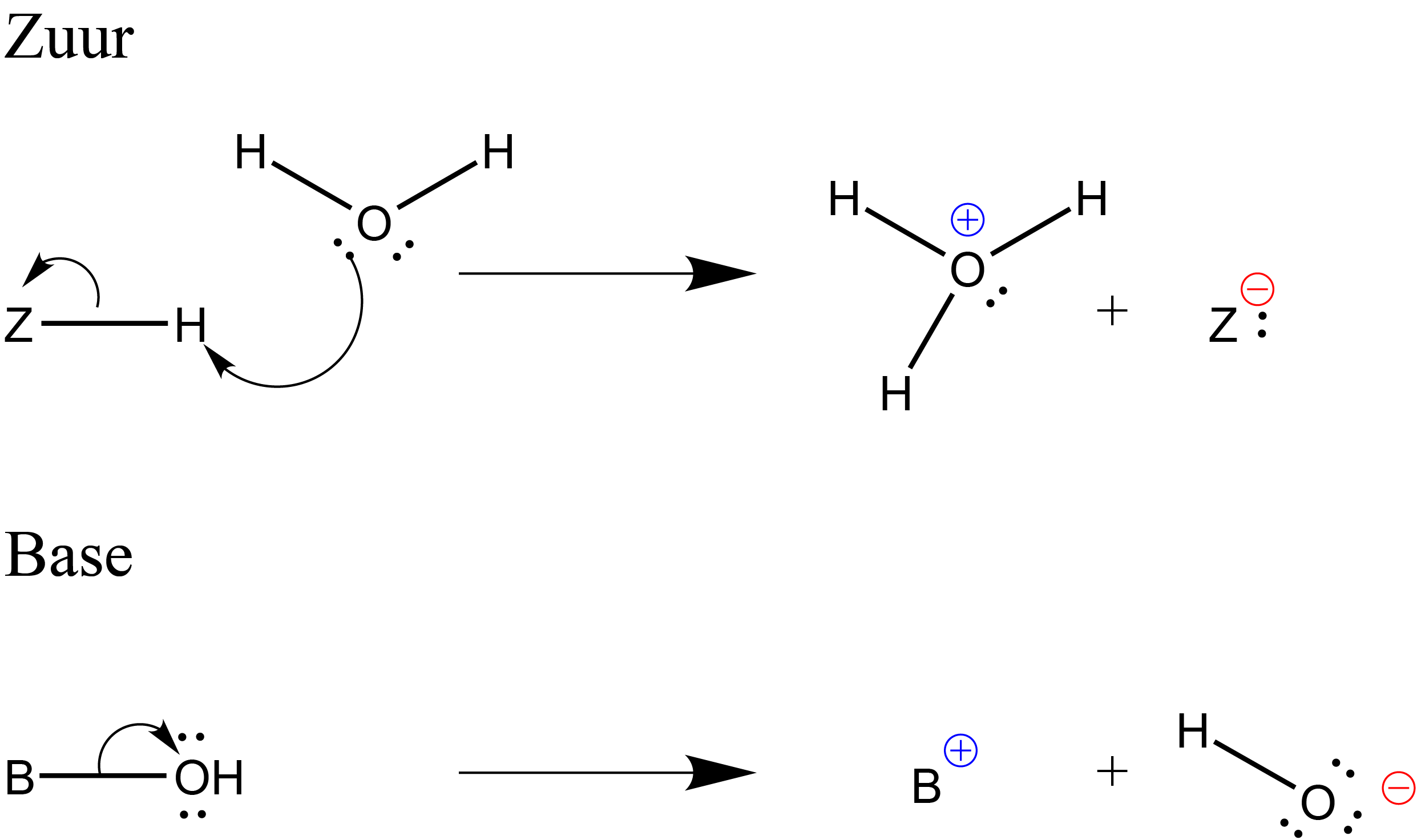
Wat gebeurt er wanneer we een zuur of base toevoegen? Laten we ons zuur even \( Z \) noemen en onze base \( B \). De reacties die plaats kunnen dan als volgt worden weergeven
Test je kennis
Omdat bij deze concentratie dan een gelijke hoeveel protonen worden afgestaan door hydroxonium ionen als er wordt opgenomen door hydroxyl-ionen.
Het evenwicht van water is de product van het aantal hydroxonium (protonen) en hydroxylionen in een oplossing.
Het aantal hydroxonium ionen neemt af en het aantal hydroxyl ionen neemt juist toe totdat zich dit evenwicht weer opnieuw heeft ingesteld. Het evenwicht blijft dus gelijk.
We lossen de vergelijking op: \[ \mathrm{1⋅10^{−14}=[OH^{−}][H_{3}O^{+}]}\] Met \( \mathrm{[OH^{−}] = 1 ⋅ 10^{-5} \mathrm{mol ⋅ L^{-1}} } \): \[ \mathrm{1⋅10^{−14}=1 ⋅ 10^{-5} \mathrm{mol⋅L^{-1}}⋅[H_{3}O^{+}]}\] Dan lossen we op: \[ \mathrm{ [H_{3}O^{+}] = \frac{1⋅10^{−14}}{1⋅10^{-5} mol⋅L^{-1} }\] \[ \mathrm{ [H_{3}O^{+}] = 1⋅10^{−9} mol⋅L^{−1} }\]
Bereken de concentratie van hydroxoniumionen in de oplossing. Ga er hierbij vanuit dat er geen verschuiving in het evenwicht plaatsvindt.
Noteer het antwoord in mol per liter met de wetenschappelijke notatie: x*10^n
