Zuren en Basen
3. pH berekenen
De zuurtegraad (pH) van een oplossing kan worden berekend door naar de activiteit (lees: concentratie) van oxonium ionen te kijken. Gezien een sterk zuur volledig ioniseert, is de concentratie van het zuur gelijk aan de concentratie hydroxonium-ionen \( \mathrm{H_{3}O^+}\) , dus de pH kan dan direct vanuit de concentratie worden berekend. \[ \mathrm{pH=−\log{\left[H_{3}O^+\right]}} \] Voor een base gelden dezelfde regels. De pOH wordt berekend door de negatieve logaritme te nemen van de concentratie hydroxyl-ionen ( \(\mathrm{OH^−}\) ) in een oplossing. \[ \mathrm{pOH=−\log{\left[OH^{−}\right]}} \] De pH en pOH kunnen ook worden berekend vanuit de evenwichtsvoorwaarde van water. Zo geldt dat, \[ \mathrm{pH=14-pOH} \] \[ \mathrm{pOH=14-pH} \]
Voorbeeld 1 - Oplossing salpeterzuur
We hebben een oplossing van 0,2 mol salpeterzuur in 500 mL water. Bereken de pH.
Stap 1. Kijk in je Binas tabel 49.
Een sterk zuur is weergeven boven de H3O+ ionen. Salpeterzuur is een sterk zuur en heeft de vergelijking
\[ \mathrm{HNO_3\left(l\right)+H_2O\left(l\right)\rightarrow H_3O^+\left(aq\right)+NO_{3}^−\left(aq\right)} \]
Stap 2. Bereken de concentratie salpeterzuur.
We rekenen van het aantal mol, naar molaire concentratie:
\[ \mathrm{\left[HNO_3\right]=\frac{0,2\ mol}{0,5\ L}=0,4\ mol\ L^{-1}=0,4\ M} \]
Stap 3: Bereken de concentratie protonen in oplossing.
We hebben te maken met een sterk zuur. Daarnaast staat salpeterzuur één \(\mathrm{H^+}\) ion (proton) af. In andere woorden:
\[ \mathrm{\left[HNO_3\right]=[H_3O^+]} \]
Stap 4: Bereken de pH
Met de concentratie protonen kunnen we pH berekenen.
\[ \mathrm{pH=-\log{\left(0,4\ mol\right)}} \]
\[ \mathrm{pH=0,39794} \]
Tot slot noteren we de pH met het juiste aantal decimalen. Het aantal decimalen is gelijk aan het aantal significante cijfers van de molaire concentratie. Met een molaire concentratie van 0,4 (één significantie cijfer), noteren we ons antwoord met één decimaal getal.
\[ \mathrm{pH}=0,4 \]
Voorbeeld 2 - Hydride-ion als base
Aan een waterige oplossing van 500 mL wordt 12,0 gram natriumhydride (NaH) toegevoegd. Bereken de pOH van de oplossing.
Als je kijkt naar de formule zou je denken dat het wel eens een zuur zou kunnen zijn, maar natriumhydride is een sterke base. Natriumhydride ioniseert in een oplossing, zoals te zien is bij alle alkalizouten (zouten met een alkalimetaal).
\[\mathrm{NaH\ \left(g\right)+H_{2}O\ \left(l\right)\rightarrow Na^+\left(aq\right)+H_{2}\left(g\right)+OH^{-}\left(aq\right)}\]
In de vergelijking is te zien dat per natriumhydride een hydroxyl-ion vrijkomt. Dus de concentratie natriumhydride is gelijk aan de concentratie hydroxylionen.
Stap 1: Bereken de concentratie hydroxyl-ionen in oplossing.
We berekenen eerst het molair gewicht van natriumhydride en deze gebruiken we om het chemisch aantal in mol te berekenen.
\[\mathrm{M_w\left(NaH\right)=22,99\ g\ mol^{-1}+1,008\ g\ mol^{-1}=23,998\ g\ mol^{-1}}\]
\[\mathrm{n\left(NaH\right)=\frac{12,0\ g}{23,998\ g\ mol^{-1}}=0,500\ mol}\]
Om de molaire concentratie te berekenen delen we door het volume van de oplossing.
\[\mathrm{c\left(NaH\right)=\frac{0,500\ mol}{0,500\ L}=1,00\ M}\]
Omdat natriumhydride volledig ioniseert in oplossing is de concentratie gelijk aan de concentratie hydride-ionen (H−) en per hydride-ion wordt een hydroxide-ion gevormd.
\[\mathrm{c\left(NaH\right)=\left[OH^{-}\right]=1,00\ M}\]
Opmerking: beide notaties zijn een weergave van de concentratie. Het verschil is dat de c(x) de theoretische concentratie aanduidt van een stof en de vierkante haakjes de werkelijke concentratie van een stof. Omdat NaH volledig ioniseert is de werkelijke concentratie vrijwel nul.
Stap 2: Bereken de pOH
Met de concentratie hydroxyl-ionen bekend kan de pOH worden berekend met de negatieve logaritme.
\[\mathrm{pOH=-\log{\left[OH^{-}\right]} }\]
\[\mathrm{pOH=-\log{\left(1,00\right)}=0,000}\]
De logaritme van 1 geeft altijd 0. Met drie significante cijfers wordt de pOH weergeven met drie decimale getallen.
3.1. Zwakke zuren
Gezien bij een zwak zuur een evenwichtsreactie ontstaat moeten er nog eerst een paar tussenberekeningen worden gedaan. We noemen ons zuur weer \(\text{Z}\). We hebben eerder geconstateerd dat zwakke zuren een evenwichtsreactie aan gaan. \[ \mathrm{ZH\left(aq\right)+H_2O\left(l\right)\rightleftarrows Z^-\left(aq\right)+H_3O^+\left(aq\right)} \] Met deze informatie kunnen we evenwichtsvoorwaarde opstellen van een zuur \(\mathrm{K_z}\). We nemen ons oplosmiddel niet mee in de vergelijking \[ \mathrm{K_z=\frac{\left[Z^-\right]\left[H_3O^+\right]}{\left[ZH\right]}}\] In bovenstaand voorbeeld gaan we ervan uit dat het zuur één proton afstaat. Dit betekent dan ook dat de concentratie van het zuur gelijk is aan dat van alle \(\mathrm{H_{3}O^+}\) ionen. In andere woorden, \[ \mathrm{\left[Z^-\right]=\left[{H_3O}^+\right]=x} \] De zuren die niet geïoniseerd zijn blijven nog over. Dus laten we de volledige concentratie van ons zuur \( \mathrm{{ZH}_{tot}}\) noemen. De concentratie van ZH is dan \[ \mathrm{\left[ZH\right]=\left[ZH_{tot}\right]-x} \] In figuur 1 is dit voorbeeld vereenvoudigd weergeven. Let op \(\mathrm{H^{+}}\) is het proton dat wordt afgestaan en is gelijk aan de \(\mathrm{H_{3}O^+}\) in de oplossing.
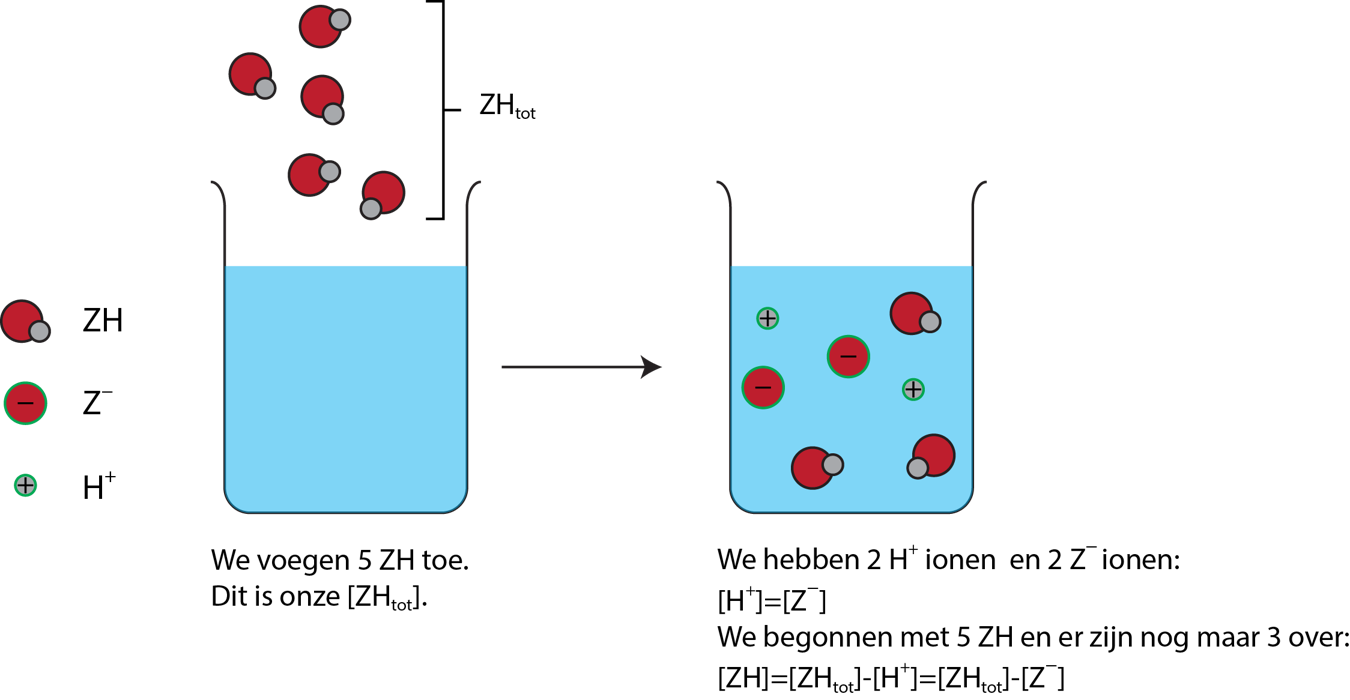
Nu kunnen we de evenwichtsvoorwaarde opnieuw opstellen \[\mathrm{K_z=\frac{x⋅x}{\left[ZH_{tot}\right]-x}=\frac{x^2}{\left[ZH_{tot}\right]-x}}\] Om de pH te bereken kunnen we twee kanten op. Dit hangt af van hoe groot de evenwichtsvoorwaarde \( (\mathrm{K_z})\) is. Bij een hele kleine \(\mathrm{K_z}\) loopt de reactie sterk naar naar links en is de concentratie van \(\mathrm{x}\) verwaarloosbaar. Wanneer de reactie meer naar rechts verloopt, dan is dit niet het geval.
In onderstaande tabel zie je de uitwerkingen bij deze verschillende \(\mathrm{K_z}\) waarden.
| \(\mathrm{K_z}\) is erg klein | \(\mathrm{K_z}\) is niet klein |
| \[\mathrm{\left[ZH_{tot}\right]-x=\left[ZH_{tot}\right]}\] \[\mathrm{K_z=\frac{x^2}{\left[ZH_{tot}\right]}}\] \[\mathrm{x=\sqrt{\left[ZH_{tot}\right]K_z}}\] \[\mathrm{pH=-\log{\left(x\right)}}\] | \[\mathrm{K_z=\frac{x^2}{\left[ZH_{tot}\right]-x}}\] \[\mathrm{x^2+K_zx-K_z\left[ZH_{tot}\right]=0}\] \[\mathrm{x=\frac{-K_z\pm\sqrt{K_z^2+4K_z\left[ZH_{tot}\right]}}{2}}\] Gezien we geen negatieve concentaties kunnen hebben, kiezen we altijd de uitkomst met een positieve x waarde. \[\mathrm{pH=-\log{\left(x\right)}}\] |
Voorbeeld 3 - pH van 1 M azijnzuur
Bereken de pH van 1 mol/L azijnzuur. We beginnen met het opstellen van de evenwichtsreactie. \[ \mathrm{CH_{3}COOH\rightleftarrows CH_{3}COO^{−}+H^+}\] Met een evenwichtsvoorwaarde van protonen in oplossing: \[ \mathrm{K_z=\frac{x^2}{1-x}}\] In de Binas vinden we een Kz van 1,8⋅10−5 voor CH3COOH. \[ \mathrm{x^2+K_{z}x-K_z=x^2+1,8⋅{10}^{−5}x-1,8⋅{10}^{−5}=0}\] \[ \mathrm{\frac{−1,8⋅{10}^{-5}\pm\sqrt{\left(1,8⋅{10}^{-5}\right)^2+4\cdot1,8⋅{10}^{-5}}}{2}}\] \[\mathrm{=\left(−0,009\pm42,3\right)⋅{10}^{-3}=4,2⋅{10}^{−3}\ of-4,2⋅{10}^{−3}}\] Gezien concentraties niet negatief kunnen zijn het aantal \(\mathrm{H_{3}O^{+}}\) ionen in de oplossing \(\mathrm{4,3⋅10^{−3} mol L^{−1}}\). Met de concentratie \(\mathrm{H_{3}O^{+}}\) kunnen we de pH berekenen: \[\mathrm{pH=-\log{\left[H_3O^+\right]}=−\log{\left(4,2⋅{10}^{−3}\right)} }\] \[\mathrm{pH=2,37}\]
Voorbeeld 4 - pOH van 1 M acetaat
Laten we de pOH berekenen van 1 M van acetaat, de geconjugeerde base van azijnzuur. We berekenen de \(\mathrm{OH^−}\) concentraties in de oplossing: \[\mathrm{k_b=\frac{x^2}{1−x}}\] In de Binas staat een Kb van \(5,5⋅10^{−10}\). \[\mathrm{x^2+5,5⋅{10}^{−10}x-5,5⋅{10}^{−10}=0}\] \[\mathrm{\frac{-5,5⋅{10}^{−10}\pm\sqrt{\left(5,5⋅{10}^{-10}\right)^2+4⋅5,5⋅10^{-10}}}{2}=\left(0,0000275\pm2,35\right)⋅{10}^{−5}}\] \[\mathrm{=\pm2,4⋅10^{−5}}\] We hebben een concentratie \(\mathrm{OH^−}\) ionen van \(2,4⋅10^{−5} \mathrm{mol⋅L^{−1}}\). Deze waarde gebruiken we om de \(\mathrm{pOH}\) te berekenen. \[\mathrm{pOH=-\log{\left[OH^-\right]}=-\log{\left(2,4⋅10^{-5}\right)}}\] \[\mathrm{pOH=4,62}\]
Test je kennis
Geef de pH met twee decimalen.
