Ruimtefiguren
1. Vormen
Ruimte figuren zijn drie-dimensionale figuren met specifieke vormen.
1.1. Prismas
Prismas zijn drie dimensionale figures die twee gelijke zijden hebben. In figuur 1 zijn voorbeelden van prismas aan de meest rechter zijde van het figuur weergeven. Prismas bevatten twee gelijke zijden, genaamd een grondvlak en bovenvlak (paarse zijden in het figuur).
Verschillende types primsa's. Deze Let op de telling en match de kleuren. Het aantal hoeken geeft de benaming van de prismas. Het aantal zijden is gelijk aan het aantal hoeken plus de grondvlak en bodemvlak.
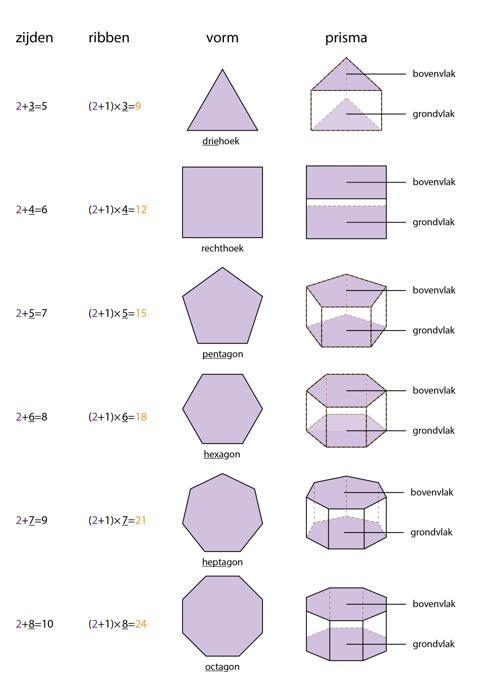
Het aantal zijden \(z\) van een ruimtelijk figuur kan worden berekend met de formule
\[z=n+2\]
waarin \(n\) staat voor het aantal zijden van het figuur zonder de bovenvlak en grondvlak mee te nemen. Deze zijn gelijk aan het aantal hoeken.
Wanneer we kijken naar een prisma (zie figuur 1 helemaal rechts), dan valt het op dat alle hoekenpunten \(h\) verbonden zijn aan 3 ribben \(r\) (lijnen). Met deze kennis kan het aantal ribben van elk figuur worden berekend met de formule
\[r=3h\]
Oftewel, hoe kan gemakkelijk het aantal ribben worden berekend?
1. Kijk naar de vorm van het bovenvlak of ondervlak. Gezien deze gelijk zijn aan elkaar in een prisma maakt het niet uit welke van de twee je kiest.
2. Nu met het aantalhoekpunten van een zijde berekend, vermenigvuldig het aantal hoekpunten met drie om het aantal ribben te berekenen.
Voorbeeld 1: Aantal zijden van een twintighoek
Bereken het totaal aantal zijden van een twintighoek.
Het aantal zijden aan de zijkanten is gelijk aan het aantal hoeken, dus als we 20 hoeken hebben dan heeft onze prisma ook 20 zijden aan de zijkant. Als we dan de grondvlak en bodemvlak meetellen, dan heeft de prisma in totaal 20+2 zijden.
Voorbeeld 2: Bereken het aantal ribben van een decagon
Een decagon bevat 10 hoeken (deca = 10). Om het aantal ribben te berekenen kijken we eerst even naar de grondvlak en bovenvlak. Gezien het aantal zijden gelijk zijn hoeft het aantal zijden maar aan een kant te worden geteld. Het aantal overstaande ribben zijn gelijk aan het aantal hoeken van het grondvlak. Dit is ook te zien in onderstaande illustratie.
Zet alle zijden onder elkaar in een tabel en tel ze allemaal bij elkaar op. Of, zoals eerder besproken is, ook hier is weer te zien dat de formule \(r = 3h \) kan worden toegepast, met \(h=10\), dus dan berekenen we \(3 \times 10 = 30 \).
1.2. Piramides
Bij prisma’s zijn twee overstaande vlakken gelijk. Zouden we het bovenvlak verwijderen door alle overstaande zijden naar een punt te laten lopen, dan krijgen we een piramide. Wat bij een primsa het grondvlak heet, wordt bij een piramide de basis genoemd. De hoogte van de piramide wordt bepaald door het punt waar de overstaande zijden elkaar kruizen.
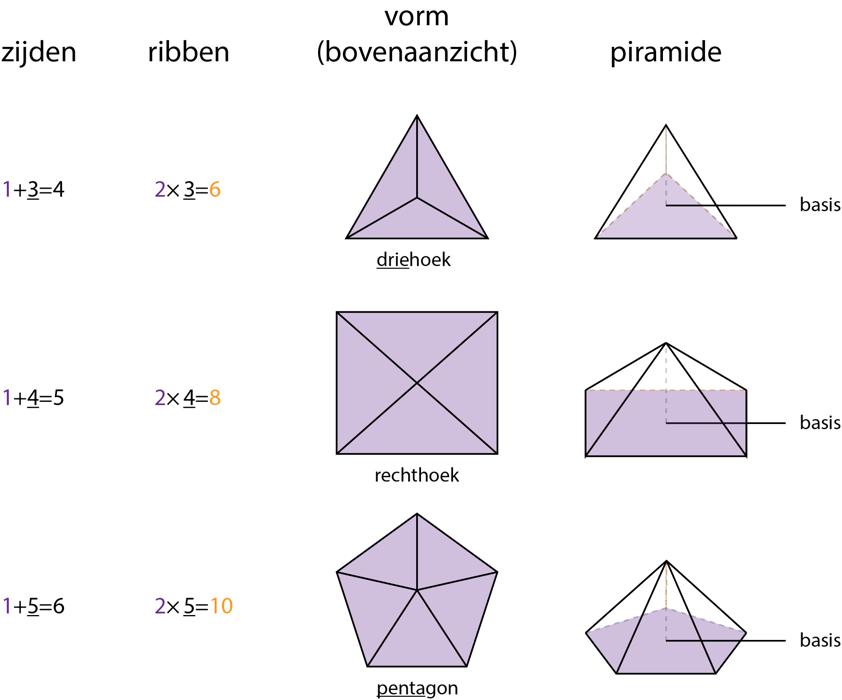
Door een bovenaanzicht van een piramide te tekenen zijn het aantal zijden en ribben worden geteld. Mocht het beeld niet zijn gegeven, dan is het goed te onthouden dat het aantal zijden van een piramide gelijk is aan de basis plus het aantal hoeken van de piramide. Het aantal ribben is een verdubbeling van het aantal hoeken van de basis van de piramide.
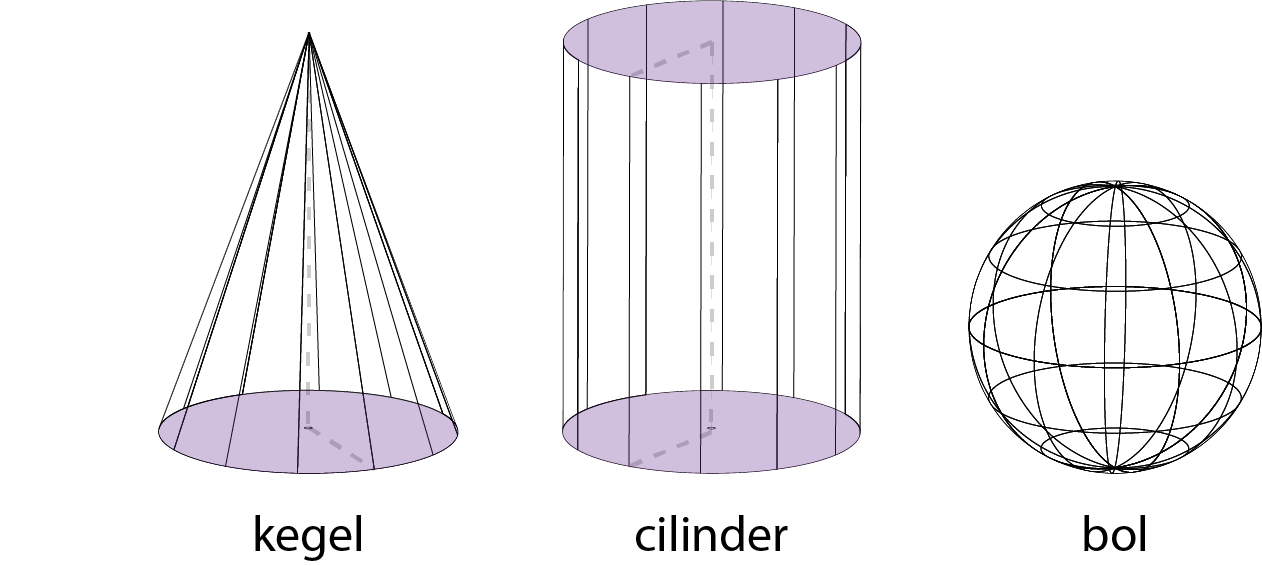
1.3. Ronde vormen
Tot zover zijn hoekige objecten besproken. Ronde vormen hebben geen hoeken. Een aantal objecten worden hier samen gevat.
Wanneer het grondvlak en bovenvlak geen hoeken bevat, maar rond zijn, dan heet het ruimteobject een cilinder.
Wanneer de basis van een piramide geen hoeken heeft, maar rond is, dan heet het object een kegel.
In bovenstaande objecten zijn hoeken te herkennen door het vanuit een zijaanzicht te bekijken. Het enige ruimteobject dat helemaal heen hoeken heeft is een bol. Dit is in alle drie dimensies rond.
Test je kennis
Test je kennis met onderstaande oefenvragen.
