Ruimtefiguren
2. Inhoud en Oppervlak
Het oppervlak van ruimtefiguren zijn te berekenen door een twee dimensionale (vlakke) weergave van het ruimtefiguur te maken, door bijvoorbeeld een uitvouwing te maken. De inhoud van een ruimteobject wordt al lastiger omdat dit afhankelijk is van het type ruimteobject. In deze sectie zullen deze twee onderdelen aan bod komen per ruimte object.
2.1. Prisma's
Gezien een prisma twee gelijke zijden heeft kan het oppervlak worden berekend door het oppervlak van het grondvlak te berekenen. Om vervolgens het gehele oppervlak te berekenen worden de zijkanten ook worden berekend. Om het oppervlak te berekenen, neen onderstaande illustratie van een uitvouwing. Het oppervlak \( A \) van een balk ik gelijk aan: \[A = 2 \cdot(l \cdot b + b \cdot h + h \cdot l) \]
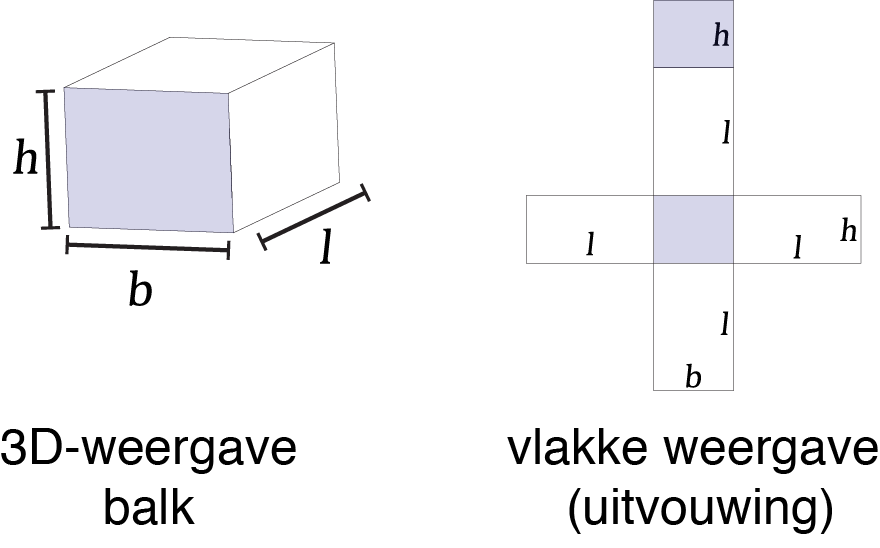
Door de inhoud te berekenen we eerst het oppervlak van het grondvlak en dit vermenigvuldigen we vervolgens met de lengte van de prisma. De formule voor de inhoud, of volume \( V \) van een prisma kan worden samengevat als \[ V = 2 \times A(grondvlak) \times l \] Dit kan worden wederom worden geïllustreerd met een balk zoals weergegeven in onderstaande afbeelding. De formule voor een balk zou dan zijn: \[ A(grondvlak) = b \times h \] \[ V(balk) = 2 \times b \times h \times l \]
Het grondvlak wordt berekend door de breedte (b) te vermenigvuldigen met de hoogte (h). Vervolgens wordt het grondvlak vermenigvuldigd met de lengte van het grondvlak.
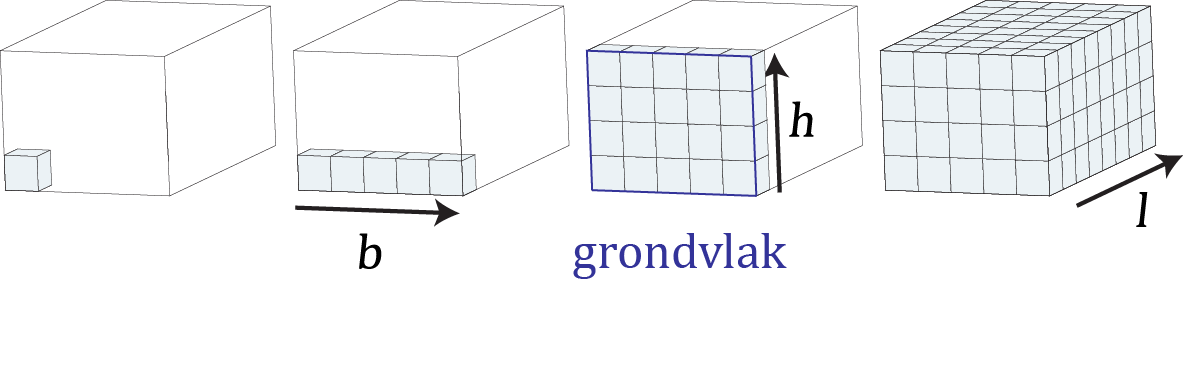
Voorbeeld 1. Bouwen van een dak
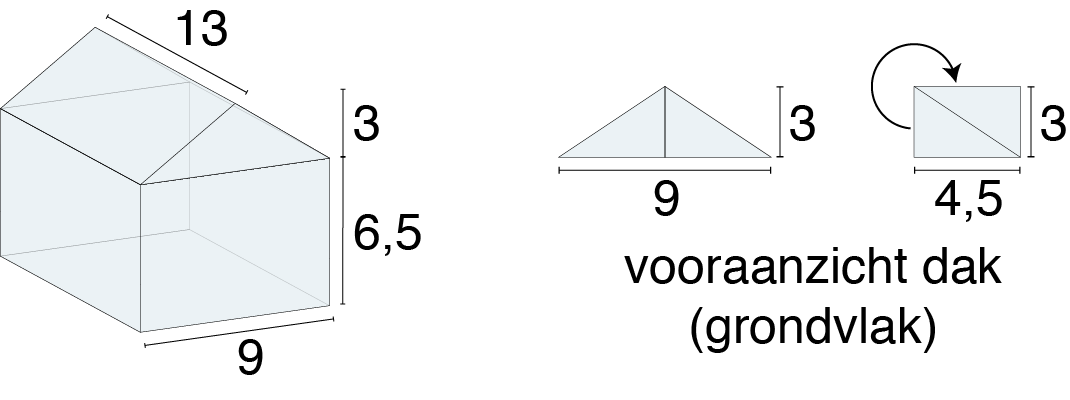
Een stel leeft in een huis met een plat dak en vragen zich af hoeveel ruimte zij erbij krijgen wanneer zij een puntdak op het huis laten zetten. De afmeting van het huis (zonder schuur) zijn 13 × 9 × 6,5 meter (zie figuur A). Ze willen een puntdak op het huis laten zetten van 3 meter hoog.
De inhoud van een driehoek is gelijk aan \( 0,5 \times b \times h\). Dus de inhoud van het dak is dan:
\[ A(grondvlak dak) = 0,5 \times 9 m \times 3 m = 13,5 m^2 \]
De inhoud van het dak is dan gelijk aan:
\[ V(dak) = 13,5 m^2 \times 13 m = 175,5 m^3 \]
Het stel zou dan \( 175,5 m^3 \) aan ruimte bij krijgen met het laten bouwen van een puntdak van 3 meter hoog.
Een ruimtelijke voorstelling van het huis is linkst van het figuur te zien. Door de inhoud van het dak te berekenen we de inhoud van de driehoek. De inhoud van een driehoek is de helft van dat van een vierkant.
Omdat in tegenstelling tot een prisma bij een piramide niet twee gelijke zijden zijn is de berekening voor het oppervlak en inhoud ook anders. Voor de inhoud moet eerst de inhoud van de schuine zijden worden berekend. Dit kan het beste worden geillustreerd door een uitvouwing te maken.
Test je kennis
We berekenen het oppervlak van alle zijden en tellen deze bij elkaar op: \[ 5 \times 2 = 10 \] \[ 2 \times 2 = 4 \] \[10 + 10 + 10 + 10 + 4 + 4 = 48\]
Bereken eerst het oppervlak van een cirkel: \[ r^2 \times \pi = \] \[ 0,5^2 \times \pi = 0,7853... \] \[ 0,7853... \times 5 = 3,9269... \] Afgerond is dit dan \( 3,93 cm^3\)
Bereken de inhoud van een bal van maat 7.
Diameter bal met maat 7: 22+2=24 cm. Met deze gegevens kan de inhoud worden berekend. \[ 24^2 \cdot \pi = 576 \cdot 3,14 = 1808,64 cm^3 \] Strategie voor hoofdrekenen: Begin eerst met het berekenen van \( 24^2 \) \[ 24(20+4) = 480+96 = 576 \] Bereken vervolgens eerst \( 576 \cdot 314 \) en deel het geheel door 100. \[ 576(300+10+4)=172800+5760+2304=180 864 \] \[ 180 764:100=1807,64 cm^3 \]